13. Chain Rule & Implicit Differentiation
Implicit Functions
An explicit function definition is an equation in which one variable is explicitly defined in terms of the other. For example, \(y=x^4\) is explicit because \(y\) is defined in terms of \(x\).
An implicit function definition is an equation relating two variables in which one variable is regarded as a function of the other. In fact, one equation can define several implicit (continuous) functions which may be distinguished by giving a point of the graph. It is usually impossible to solve an implicit definition to give an explicit definition of the function.
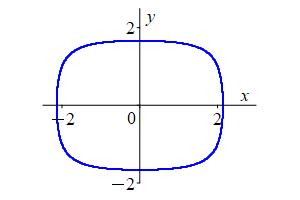
As an example, the graph of the equation \(x^4+x^2y^2+y^6=21\) is shown at the right. The equation implicitly defines \(y\) as many different continuous functions of \(x\). The upper half of the graph is the function passing through \((x,y)=(2,1)\) while the lower half is the function passing through \((x,y)=(2,-1)\). (Check \((2,1)\) and \((2,-1)\) are solutions to the equation.)
d. Implicit Differentiation
We would like to compute the derivatives of implicitly defined functions so that we can construct tangent lines. We do this by example.
The equation \(x^4+x^2y^2+y^6=21\) implicitly defines \(y\) as a function of \(x\) which passes through the point \((x,y)=(2,1)\). Compute \(\dfrac{dy}{dx}\) at \((2,1)\) and find the tangent line.
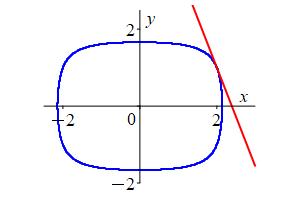
We first check that \((x,y)=(2,1)\) is a solution to the equation: \[ x^4+x^2y^2+y^6=(2)^4+(2)^2(1)^2+(1)^6=16+4+1=21 \] We start by rewriting the equation indicating that we regard \(y\) as a function of \(x\): \[ x^4+x^2y_{(x)}^{\enspace2}+y_{(x)}^{\enspace6}=21 \] Notice that we wrote the \((x)\) small because we don't usually write it; we just think it. Now we take the \(x\) derivative of both sides, i.e. we apply the operator \(\dfrac{d}{dx}\) to both sides. We include many more steps than necessary, to make it clear how we are applying the Sum, Product, Power and Chain Rules: \[\begin{aligned} \dfrac{d}{dx}(x^4)+\dfrac{d}{dx}(x^2y^2)+\dfrac{d}{dx}(y^6) =\dfrac{d}{dx}(21)& \qquad \text{Sum Rule} \\ \dfrac{d}{dx}(x^4)+\dfrac{d}{dx}(x^2)y^2+x^2\dfrac{d}{dx}(y^2) +\dfrac{d}{dx}(y^6) =0& \qquad \text{Product Rule} \\ 4x^3+2xy^2+x^22y\dfrac{dy}{dx}+6y^5\dfrac{dy}{dx} =0& \qquad \text{Power and Chain Rules (*)} \end{aligned}\] Notice that \(y\) is a function of \(x\). So the derivatives \(\dfrac{d}{dx}(y^2)\) and \(\dfrac{d}{dx}(y^6)\) are done by Chain Rule and we write \(\dfrac{dy}{dx}\) for the derivative of the inner function. We now solve for \(\dfrac{dy}{dx}\) by grouping terms. \[ (2x^2y+6y^5)\dfrac{dy}{dx}=-4x^3-2xy^2 \] \[ \dfrac{dy}{dx}=\dfrac{-4x^3-2xy^2}{2x^2y+6y^5} \qquad \qquad \text{(**)} \] Finally, we evaluate the derivative at \((x,y)=(2,1)\). \[ \left.\dfrac{dy}{dx}\right|_{(2,1)} =\dfrac{-32-4}{8+6} =-\,\dfrac{18}{7} \] We use the point-slope formula to find the equation of the tangent line at \((x_o,y_o)=(2,1)\): \[ y=y_o+m(x-x_o) =1-\dfrac{18}{7}(x-2) \]
Notice that the derivative given in equation (**) depends on both \(x\) and \(y\). You need to know both coordinates to be able to find the derivative at a point on the graph.
If you are only interested in finding the derivative at a single point, then it is usually simpler to plug numbers into equation (*) rather than equation (**). This avoids algebra mistakes. At \((x,y)=(2,1)\), equation (*) becomes: \[ 32+4+8\dfrac{dy}{dx}+6\dfrac{dy}{dx}=0 \quad \Rightarrow \quad \left.\dfrac{dy}{dx}\right|_{(2,1)}=-\,\dfrac{18}{7} \]
Here's an alternate way to think about the tangent line.
The original equation, \(x^4+x^2y^2+y^6=21\), implicitly defines \(y\) as
a function of \(x\) which passes through the point \((x,y)=(2,1)\).
This means \(f(2)=1\) and \(f'(2)=\left.\dfrac{dy}{dx}\right|_{(2,1)}\).
We can use these in the general equation of the tangent line:
\[
y=f(2)+f'(2)(x-2)=1-\dfrac{18}{7}(x-2)
\]
The equation \(x^2y^3+xy^2=12\) implicitly defines \(y\) as a function of \(x\) which passes through the point \((x,y)=(1,2)\). (Check \((x,y)=(1,2)\) is a solution to the equation.) Compute \(\dfrac{dy}{dx}\) at \((1,2)\) and find the tangent line.
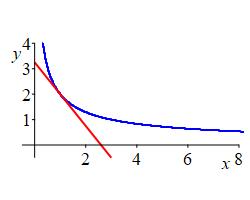
\(\left.\dfrac{dy}{dx}\right|_{(1,2)}=-\,\dfrac{5}{4}\)
\(y=2-\dfrac{\rule{0pt}{10pt}5}{4}(x-1)=-\,\dfrac{5}{4}x+\dfrac{13}{4}\)
We first check that \((x,y)=(1,2)\) is a solution to the equation. \[ x^2y^3+xy^2=(1)^2(2)^3+(1)(2)^2=8+4=12 \] We apply the operator \(\dfrac{d}{dx}\) to both sides, using the Product and Chain Rules: \[ (2x)y^3+x^2 3y^2\dfrac{dy}{dx} +(1)y^2+x 2y\dfrac{dy}{dx} =0 \] Now we evaluate at \((x,y)=(1,2)\) and solve for the derivative: \[ 16+12\dfrac{dy}{dx}+4+4\dfrac{dy}{dx}=0 \] \[ f'(1)=\left.\dfrac{dy}{dx}\right|_{(1,2)}=-\,\dfrac{20}{16}=-\,\dfrac{5}{4} \] Since \(f(1)=2\), the tangent line is: \[\begin{aligned} y&=f(1)+f'(1)(x-x_o) =2-\dfrac{5}{4}(x-1) \\ &=-\,\dfrac{5}{4}x+\dfrac{13}{4} \end{aligned}\]
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum